8 广义线性混合效应模型
8.1 离散(discrete)数据 vs. 连续(continuous)数据
到目前为止,我们考虑的所有模型都假设测量的响应变量(即因变量)是连续的且是数值型的。然而,在心理学中,很多情况下我们的测量结果是离散的。离散数据的一种类型是可能值的有限值集合,且可能值之间有间隔,例如使用李克特量表获得的数据。另一种类型的离散数据是响应变量反映没有内在顺序的类别(通常称为“名义(nominal)”数据),例如餐馆顾客点的是鸡肉、牛肉还是豆腐。
离散数据在心理学中很常见。以下是一些离散数据的例子:
- 说话者产生的语言结构类型(双宾语结构或介词短语结构);
- 被试在给定时间内观看的是哪一组图像;
- 被试是否做出了准确或不准确的选择;
- 求职者是否被录用;
- 李克特量表上的同意度。
另一种常见的数据类型是计数数据,其中数值也是离散的。通常在计数数据中,某件事发生的机会数量没有明确定义。一些例子:
- 自然语言语料库中的语误次数;
- 每年在某个路口发生的交通事故次数;
- 在给定月份中看医生的次数。
8.1.1 为什么不将离散数据建模为连续数据?
离散数据具有一些特性,这些特性通常使得尝试使用连续数据模型来分析它们变得不合适。例如,如果你对某些二元事件(被试在强制选择任务中的准确性)的概率感兴趣,每次测量将表示为0或1,分别表示不准确或准确的响应。你可以计算每个被试的准确响应比例并分析它(确实很多人这么做),但这是一个糟糕的想法,原因有很多。
8.1.1.1 有界尺度(dounded scale)
离散数据通常具有有界尺度。它可能是有下界的(如计数数据下界为0),也可能同时有上界和下界(如李克特量表数据或二元数据)。如果你尝试使用为连续数据设计的方法来建模有界数据,那么模型可能最终将非零概率分配给尺度之外的不可能值。
使用连续数据模型分析有界数据可能会导致虚假的交互效应。例如,考虑某种实验干预对准确性的影响。如果被试在条件A中已经非常准确(如超过90%),而在条件B中较低(如50%),那么(干预)在A中的可能效果很可能小于在B中的可能效果,因为准确性不能超过100%。因此,很难确定交互效应是反映了理论上有意义的东西,还是单纯是尺度有界的产物。
8.1.1.2 方差依赖于均值
在大多数连续数据设置中,通常假设方差与均值无关;这本质上是对含有连续预测变量的模型的方差齐性(homogeneity of variance)假设。对于离散数据,这种方差独立于均值的假设通常不成立。
我们可以通过数据模拟看到这一点。rbinom()函数可以模拟二项分布的数据,该分布描述了一组行为的离散观测值。让我们考虑一下巴塞罗那(Barcelona, Spain)和格拉斯哥(Glasgow, U.K)在某一天的降雨概率。根据这个网站,巴塞罗那每年平均有55天下雨,而格拉斯哥有170天。因此,格拉斯哥某一天的降雨概率可以估计为170/365,大约是0.47,而巴塞罗那的概率是55/365,大约是0.15。让我们模拟500年的降雨数据(假设气候恒定)。
rainy_days <- tibble(city = rep(c("Barcelona", "Glasgow"), each = 500),
days_of_rain = c(rbinom(500, 365, 55/365),
rbinom(500, 365, 170/365))) 如果我们看一下每个城市模拟数据的标准差,我们可以看到格拉斯哥的变异性更大。
## # A tibble: 2 × 2
## city variance
## <chr> <dbl>
## 1 Barcelona 46.5
## 2 Glasgow 90.0对于二项分布的数据,方差由\(np(1-p)\)给出,其中\(n\)是观测次数,\(p\)是“成功”的概率(上述例子中某一天降雨的概率)。下图显示了\(n=1000\)的情况;注意,当概率接近0和1时,方差变得很小,而在0.5处达到峰值。
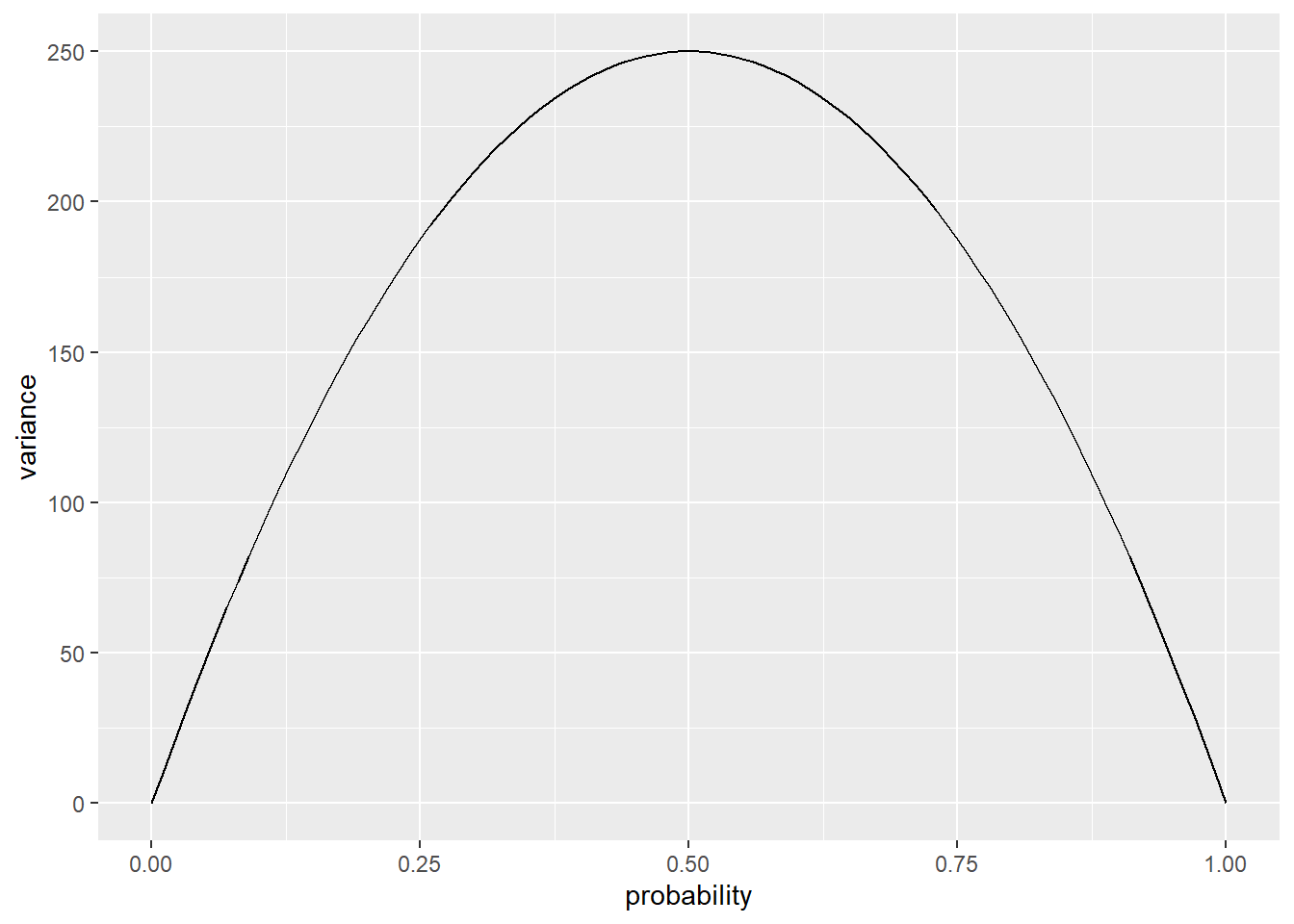
图8.1: 方差与概率的关系图(\(n=1000\))
8.2 广义线性模型
广义线性模型[不要与一般线性模型(General Linear Models)混淆]的基本思想是指定一个链接函数(link function),将响应空间(response space)转换为建模空间(modeling space),这样我们可以执行常规线性回归,并通过方差函数(variance function)捕捉方差对均值的依赖性。模型的参数将在建模空间的尺度上表示,但我们总是可以使用逆链接函数(inverse link function)将其转换回原始的响应空间。
有很多不同类型的广义线性模型可以拟合不同类型的数据。在心理学中最常用的是逻辑回归(logistic regression)和泊松回归(Poisson regression),前者用于二分类数据(伯努利试验,Bernoulli trials),后者用于试验次数未明确规定计数数据。我们将重点关注逻辑回归。
8.3 逻辑回归
8.3.1 术语
| Term | Definition |
|---|---|
| 伯努利试验 | 具有二元结果的事件,其中一个结果被认为是“成功” |
| 概率(proportion) | 伯努利试验的成功次数与总次数之比 |
| 发生比(odds) | 成功对失败的比率 |
| 对数发生比(log odds) | 发生比的(自然)对数 |
注:odds也有人翻译为几率,考虑到几率表意并不直观,且易与概率(proportion)混淆,发生比又有些拗口,很多材料也不去翻译,所以本文之后直接使用odds和log odds。
在逻辑回归中,我们在log odds空间中建模响应变量与一组预测变量之间的关系。
逻辑回归用于个体结果是伯努利试验(具有二分类结果的事件)的情况。通常两种结果之一被称为“成功”,编码为1;另一种结果称为“失败”,编码为0。需要注意的是,“成功”和“失败”这两个术语是完全随意的,不应该认为更可取的类别总是编码为1。例如,当抛硬币时,我们可以同样选择“正面”为成功,“反面”为失败,反之亦然。
通常,伯努利试验序列的结果通过概率(成功次数与试验总次数的比率)来传达。例如,如果我们抛硬币100次,得到47次正面,那么我们的概率就是47/100或0.47,这也将是我们对事件可能性的估计。对于编码为1和0的事件,计算概率的便捷方法是使用mean()函数。
我们也可以谈论成功的odds,例如,正面与反面的odds是一比一,即1:1。格拉斯哥某天降雨的odds是170:195;分母是没有下雨的天数(365 - 170 = 195)。用小数表示,170/195约等于0.87,这被称为natural odds。natural odds的范围是0到\(+\infty\)。给定\(N\)次试验中成功\(Y\)次,我们可以将natural odds表示为\(\frac{Y}{N - Y}\)。或者,给定一个概率\(p\),我们可以将odds表示为\(\frac{p}{1-p}\)。
odds的自然对数,或logit,是进行逻辑回归的尺度。回想一下,对某个值\(Y\)的对数给出在给定底数下使\(Y\)成立的指数。例如,16的\(log_2\)(以2为底的对数)是4,因为\(2^4 = 16\)。在逻辑回归中,通常使用的底数是\(e\)(也称为欧拉数,Euler’s number)。例如,要从格拉斯哥降雨的odds中得到log odds,我们会使用log(170/195),其结果为-0.1372011;要从log odds中恢复natural odds,我们会使用逆运算exp(-.137),其结果约为0.872。
8.3.2 log odds的性质
log odds = \(\log \left(\frac{p}{1-p}\right)\)
log odds具有一些适用于线性建模的优秀性质。
首先,它是围绕0对称,且log odds等于0对应最大的不确定性,即概率为0.5。正的log odds意味着成功比失败更可能(成功的概率 > 0.5),负的log odds意味着失败比成功更可能(成功的概率 < 0.5)。log odds为2表示成功比失败可能性大的程度与-2表示失败比成功可能性大的程度相同。其尺度是无界的,范围从\(-\infty\)到\(+\infty\)。
8.3.3 链接函数和方差函数
逻辑回归的链接函数是:
\[\eta = \log \left(\frac{p}{1-p}\right)\]
而逆链接函数为:
\[p = \frac{1}{1 + e^{-\eta}}\]
其中\(e\)是欧拉数。在R中,In R, 你可以将逆链接函数写成:1/(1 + exp(-eta))。
方差函数为二项分布的方差,即:
\[np(1 - p)\]
下面的app允许你在log odds空间中操控一条线的截距和斜率,并查看该线在响应空间中的投影。请注意该函数在响应空间中是S形(“sigmoidal”)。
图8.2: 逻辑回归网页app https://rstudio-connect.psy.gla.ac.uk/logit
8.3.4 在R中估计逻辑回归模型
对于单层数据,可以使用glm()函数。请注意,这个函数与你已经熟悉的lm()函数非常相似。主要区别在于你需要为链接/方差函数指定一个family参数。对于逻辑回归,可以使用family = binomial(link = "logit")。二项分布的链接默认值是logit链接,因此只需输入family = binomial即可。
glm(DV ~ IV1 + IV2 + ..., data, family = binomial)
对于有随机效应的多层数据,可以使用lme4包中的glmer函数:
glmer(DV ~ IV1 + IV2 + ... (1 | subject), data, family = binomial)
## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr 1.1.4 ✔ readr 2.1.5
## ✔ forcats 1.0.0 ✔ stringr 1.5.1
## ✔ ggplot2 3.5.0 ✔ tibble 3.2.1
## ✔ lubridate 1.9.3 ✔ tidyr 1.3.1
## ✔ purrr 1.0.2
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag() masks stats::lag()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors